A×10n の形で表す。Aを仮数部、nを指数部、10を基数という。 Aは絶対値が1以上10未満(1/10以上1未満の場合もあり、基数が変われば当然これらも変わってくる) この形ですべての小数を表す。この形になっていない数字は、Aとnを調節してこの条件に合うように調節する。 この操作を浮動小数点の正規化(Regulate)という。プログラミング時は、基数は勝手に想定することにしてAとnを保持するようにする。 この浮動小数点を用いた加減乗除演算を作る。このとき演算により正規化されていないものが出てくるので、 その場合は正規化処理を施す必要がある。
浮動小数点のビット表現はIEEE754-1985で標準化されている。64ビット時は、基数は2、最上位1ビットが符号、続く16ビットが指数(バイアス表記)、 残り47ビットで仮数(絶対値表記)となる。符号は0が正1が負、指数は実際の値より215大きい数字による表記(バイアス表記)でこれによりすべて非負正数表記となる。 仮数は1/2以上1未満となるように正規化されていて、最上位ビットは必ず1となるのでこれを省略したものを表記する。これにより実質48ビット精度となる。
上の「myMath」はIEEEには全然従ってません。。
数学の専門家じゃないので、正確には説明できません〜 高校レベルの関数に対する知識があればまぁもんだいないでしょう。
ある関数f(x)が無限回微分可能なとき、関数f(x)を以下のように表すことができる。これをテイラー展開という。
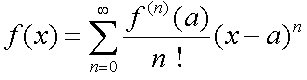
a=0かa=1のものがよく使われる。a=0のものを特にマクローリン展開という。
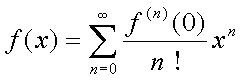
この式においてnが十分に大きい場合に項が限りなく0に近づけば、適当なnまでを計算することで数値的近似値を出すことができる。
a=0のものを使用する。
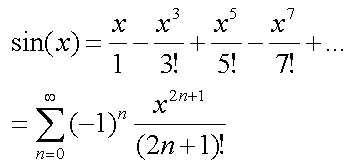
当然だけど、ここではすべて弧度法(ラジアン単位)です。
a=0のものを使用する。
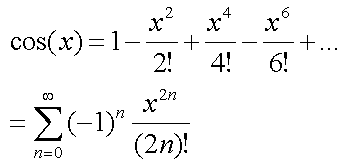
tan(x) = sin(x) / cos(x) よりtanも求めることができる。
xがそれなりに大きな数字(マイナスに小さすぎるのも含む)の場合は収束が遅くなるので、位相を2πずらしても値が変わらない、
πずらして正負反転、π/2ずらしのsin<->cos変換を利用してできるだけ0周りに寄せる、という小技を使う。
(π=3.141592653589793 ... くらい)
a=0のものを使用する。
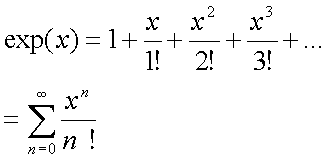
xが大きい(マイナスに小さすぎるのも含む)と収束が遅くなるので、exp(x) = exp(x-1) * e を用いてできるだけ-1〜1までの間に寄せる。
(e=2.718281828459045 ... くらい)
a=1のものを使用する。a=0のものはlog(0)がでてくるので使えない。
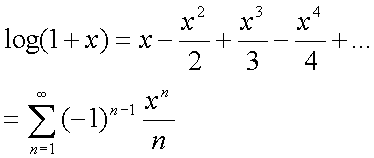
x絶対値が1より大きいとと収束しなくなるので、log(x) = 1 + log(x/e) を用いてできるだけ-1〜1までの間に寄せる。
x<=-1 の時計算不能。JavaではArithmeticExceptionの例外を投げればよい。
a=0のものを使用する。
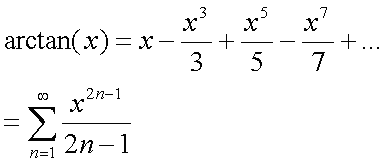
x絶対値が1以下じゃないと収束しないので、arctan(x)=π/2-arctan(1/x) を利用して-1〜1に寄せる。
a=0のものを使用する。
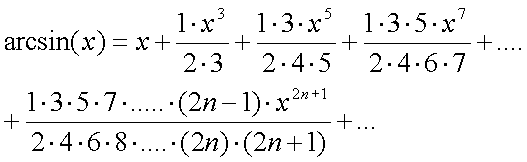
arcsin(x) + arccos(x) = π/2 を利用してarccosを求めることができる。
|x|>1 の時計算不能。JavaではArithmeticExceptionの例外を投げればよい。
a=0のものを使用する。
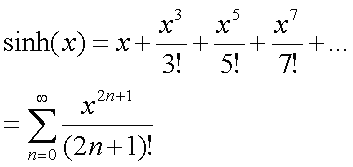
sinh(x) = {exp(x)-exp(-x)} / 2 と定義されるので、expの展開を利用してそのまま求めることもできる。
a=0のものを使用する。
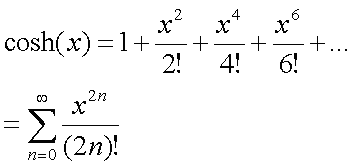
cosh(x) = {exp(x)+exp(-x)} / 2 と定義されるので、expの展開を利用してそのまま求めることもできる。
tanh(x) = sinh(x) / cosh(x) により、tanhも求められる。
以下のニュートン法を用いる。
f(x)が微分可能でf(x)=0の解が存在するとき、以下により求まる数列{ x[n] }の極限がf(x)=0の解になる。初期値x[0]は適当な値aとする。
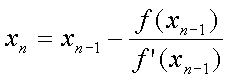
数値計算上では、nを十分な大きさまでとってやればよい。
f(x) = x2-aとしてこのニュートン法を適用する。以下の数列の極限値がaの平方根となっている。初期値はx[0]=aが妥当。
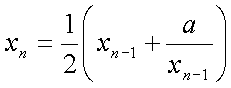
以下で述べる任意の底の任意乗を用いても求めることができるが、ニュートン法の方が一般的で計算も速い。
指数関数と対数関数を用いて展開することができる。
![]()
log(p)は求めることができ、q*log(p)も求めることができるので、exp{q*log(p)}も求めることができる。
よってこれにより展開することが可能である。